The DEAN’S COLUMN
Crossing the Bridges
By Alfred Posamentier, Ph.D.
New York City, which is comprised mostly of islands (as a matter of fact the only part of the city that is part of the mainland of the United States is the main part of the Bronx—of course, excluding City Island), is blessed with many bridges. We have bike and track races that traverse several bridges throughout the tour. One takes bridge crossing for granted these days. They essentially become part of the path traveled and don’t become noticed unless there is a toll to be paid. Then one takes particular note of the bridge crossing.
In the eighteenth century and earlier, when walking was the dominant form of local transportation, people would often count particular kinds of objects they passed. One such was bridges.
Through the eighteenth century the small Prussian city of Königsberg (today called Kaliningrad, Russia), located where the Pregel River formed two branches, was faced with a recreational dilemma: Could a person walk over each of the seven bridges exactly once in a continuous walk through the city? The residents of the city had this as a recreational challenge, particularly on Sunday afternoons. Since there were not successful attempts, the challenge continued for many years.
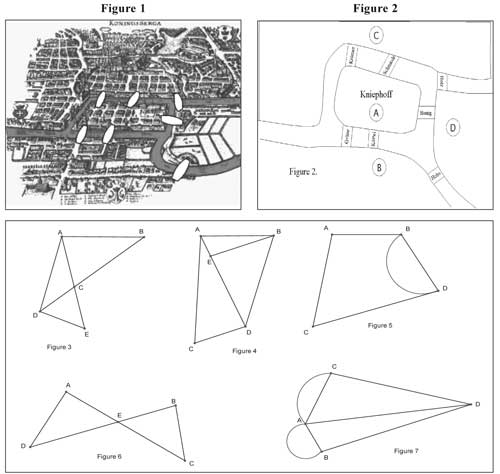
This problem provides a wonderful window into an extended field of geometry—a course that this semester will be getting much more attention in the schools of New York State. To begin we should present the problem. In Figure 1 we can see the map of the city with the seven bridges highlighted.
In Figure 2, we will indicate the island by A, the left bank of the river by B, the right one by C, and the area between the two arms of the upper course by D. If we start at Holz and walk to Schmiede and then through Honig, through Hohe, through Köttel, through Grüne we will never cross Krämer. On the other hand if we start at Krämer and walk to Honig, through Hohe, through Köttel, through Schmiede, through Holz we will never travel through Grüne.
In 1735 the famous mathematician Leonhard Euler (1707-1783) proved mathematically that this walk could not be performed. Indicate to students that the ensuing discussion will tie in their earlier work with networks to the solution of the Königsberg Bridge Problem.
The famous Königsberg Bridges Problem is a lovely application of a topological problem with networks. It is very nice to observe how mathematics used properly can put a practical problem to rest. Before we embark on the problem we ought to become familiar with the basic concept involved. Toward that end, have students try to trace with a pencil each of the following configurations without missing any part and without going over any part twice. Ask students to determine the number of arcs or line segments, which have an endpoint at each of the points: A, B, C, D, E.
Configurations such as the five figures above are made up of line segments and/or continuous arcs are called networks. The number of arcs or line segments that have an endpoint at a particular vertex, is called the degree of the vertex.
After trying to trace these networks without taking their pencils off the paper and without going over any line more than once, students should notice two direct outcomes. The networks can be traced (or traversed) if they have (1) all even degree vertices or (2) exactly two odd degree vertices. The following two statements establishes this.*
1. There is an even number of odd degree vertices in a connected network.
2. A connected network can be traversed, only if it has at most two odd degree vertices.
Have students now draw both traversable and nontraversable networks (using these two theorems).
Network Figure 3 has five vertices. Vertices B, C, E are of even degree and vertices A and D are of odd degree. Since Figure I has exactly two odd degree vertices as well as three even degree vertices it is traversable. If we start at A then go down to D, across to E, back up to A, across to B, and down to D we have chosen a desired route.
Network Figure 4 has five vertices. Vertex C is the only even degree vertex. Vertices A, B, E, and D, are all of odd degree. Consequently, since the network has more than two odd vertices, it is not traversable.
Network Figure 5 is traversable because it has two even vertices and exactly two odd degree vertices.
Network Figure 6 has five even degree vertices and can be traversed.
Network Figure 7 has four odd degree vertices and cannot be traversed.
The Königsberg Bridge Problem is the same problem as the one posed in Figure 7. Let's take a look at Figures 2 and 7 and note the similarity. There are seven bridges in Figure 2 and there are seven lines in Figure 7. In Figure 7 each vertex is of odd degree. In Figure 6 if we start at D we have three choices, we could go to Hohe, Honig, or Holz. If in Figure 7 we start at D we have three line paths to choose from. In both figures if we are at C we have either three bridges we could go on or three lines. A similar situation exists for locations A and B in Figure 6 and vertices A and B in Figure 7. Emphasize that this network cannot be traversed.
By reducing the bridges and islands to a network problem we can easily solve it. This is a clever tactic to solve problems in mathematics. You might try to find a group of local bridges to create a similar challenge and see if the walk is traversable. This problem and its network application is an excellent introduction into the field of topology.#
Dr. Alfred Posamentier is Dean of the School of Education at City College of NY, author of over 40 Mathematics books including: “Math Wonders to Inspire Teachers and Students” (ASCD, 2003) and “The Fabulous Fibonacci Numbers” (Prometheus, 2007), and member of the NYS Mathematics Standards Committee.
________________________
* The proof of these two theorems can be found in A. S. Posamentier and J. Stepelman, Teaching Secondary School Mathematics: Techniques and Enrichment Units (Columbus, Ohio: Prentice Hall/Pearson, 7th ed. 2006).