THE DEAN'S COLUMN
A Source for Mathematical Insights:
The Hands of A Clock
By Alfred Posamentier, Ph.D.
The clock can be an interesting source of mathematical applications. Applications do not always have to show how useful mathematics is in other disciplines. In this case we can see how the clock provides students with a rich source of some problem-solving skills that give some further meaning to “uniform motion.”
Begin by asking your students to determine the exact time that the hands of a clock will overlap after 4:00 o’clock. Your students’ first reaction to the solution to this problem likely will be that the answer is simply 4:20.
When you remind them that the hour hand moves uniformly slowly, while the minute hand moves faster, they will begin to estimate the answer to be between 4:21 and 4:22. They should realize that the hour hand moves through an interval between minute markers every 12 minutes. Therefore it will leave the interval 4:21 - 4:22 at 4:24. This however doesn’t answer the original question about the exact time of this overlap.
Once they realize that this is not the correct answer, since the hour hand does not remain stationary and moves when the minute hand moves. You could show them a “trick,” which is simply multiply the 20 (the wrong answer) by 12 / 11 to get 21(9 / 11), which yields the correct answer: 4:21(9 / 11).
One way to have students begin to understand the movement of the hands of a clock is by having them consider the hands traveling independently around the clock at uniform speeds. The minute markings on the clock (from now on referred to as “markers”) will serve to denote distance as well as time. An analogy should be drawn here to the “uniform motion” of automobiles (a popular topic for verbal problems in an elementary algebra course). A problem involving a fast automobile overtaking a slower one would be analogous.
Experience has shown that the analogy might be helpful to have the class find the distance necessary for a car traveling at 60 m.p.h. to overtake a car with a head start of 20 miles and traveling at 5 m.p.h.
Now have the class consider 4 o’clock as the initial time on the clock. Our problem will be to determine exactly when the minute hand will overtake the hour hand after 4 o’clock. Consider the speed of the hour hand to be r, then the speed of the minute hand must be 12r. We seek the distance, measured by the number of markers traveled, that the minute hand must travel to overtake the hour hand.
Let us refer to this distance as d markers. Hence the distance that the hour hand travels is d–20 markers, since it has a 20-marker head start over the minute hand.
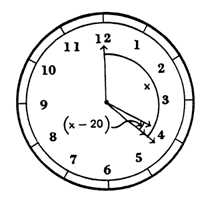
For this to take place, the times required for the minute hand, d / (12r), and for the hour hand, (d – 20)/r, are the same. Therefore, d / (12r) = (d – 20) / r, and d = (12 / 11) ·20 = 21 (9 / 11). Thus the minute hand will overtake the hour hand at exactly 4:21(9 / 11).
Consider the expression d = (12 / 11) ·20. The quantity 20 is the number of markers that the minute hand had to travel to get to the desired position, if we assume the hour hand remained stationary. However, quite obviously, the hour hand does not remain stationary. Hence, we must multiply this quantity by 12 / 11, since the minute hand must travel 12 / 11 as far. Let us refer to this fraction, 12 / 11, as the correction factor. You might wish to have the class verify this correction factor both logically and algebraically.
To begin to familiarize the students with use of the correction factor, choose some short and simple problems. For example, you may ask them to find the exact time when the hands of a clock overlap between 7 and 8 o’clock. Here the students would first determine how far the minute hand would have to travel from the “12” position to the position of the hour hand, assuming again that the hour hand remains stationary. Then by multiplying the number of markers, 35, by the correction factor, 12 / 11, they will obtain the exact time, 7:38 (2 / 11), that the hands will overlap.
To enhance students’ understanding of this new procedure ask them to consider a person checking a wristwatch against an electric clock and noticing that the hands on the wristwatch overlap every 65 minutes (as measured by the electric clock). Ask the class if the wristwatch is fast, slow, or accurate.
You may wish to have them consider the problem in the following way. At 12 o’clock the hands of a clock overlap exactly. Using the previously described method we find that the hands will again overlap at exactly 1:05 (5 / 11), and then again at exactly 2:10 (10 / 11), and again at exactly 3:16 (4 / 11) and so on. Each time there is an interval of 65 (5 / 11) minutes between overlapping positions. Hence, the person’s watch is inaccurate by 5 / 11 of a minute. Have students now determine if the wristwatch is fast or slow.
There are many other interesting, and sometimes rather difficult, problems made simple by this “correction factor.” You may very easily pose your own problems. For example, you may ask your students to find the exact times when the hands of a clock will be perpendicular (or form a straight angle) between, say, 8 and 9 o’clock.
Again, you would have the students determine the number of markers that the minute hand would have to travel from the “12” position until it forms the desired angle with the stationary hour hand. Then have them multiply this number by the correction factor, 12 / 11, to obtain the exact actual time. That is, to find the exact time that the hands of a clock are first perpendicular between 8 and 9 o’clock, determine the desired position of the minute hand when the hour hand remains stationary (here, on the 25 minute marker). Then, multiply 25 by 12 / 11 to get 8:27 (3 / 11) , the exact time when the hands are first perpendicular after 8 o’clock.
For students who have not yet studied algebra, you might justify the 12/11 correction factor for the interval between overlaps in the following way:
Think of the hands of a clock at noon. During the next 12 hours (i.e. until the hands reach the same position at midnight) the hour hand makes one revolution, the minute hand makes 12 revolutions, and the minute hand coincides with the hour hand 11 times (including midnight, but not noon, starting just after the hands separate at noon).
Since each hand rotates at a uniform rate, the hands overlap each 12 / 11 of an hour, or 65 (5 / 11) minutes.
This can be extended to other situations.
Your students should derive a great sense of achievement and enjoyment as a result of employing this simple procedure to solve what usually appears to be a very difficult clock problem.#
Dr. Alfred Posamentier is Dean of the School of Education at City College of NY, author of over 40 Mathematics books including: Math Wonders to Inspire Teachers and Students (ASCD, 2003) and The Fabulous Fibonacci Numbers (Prometheus, 2007), and member of the NYS Mathematics Standards Committee.
