The Dean's Column:


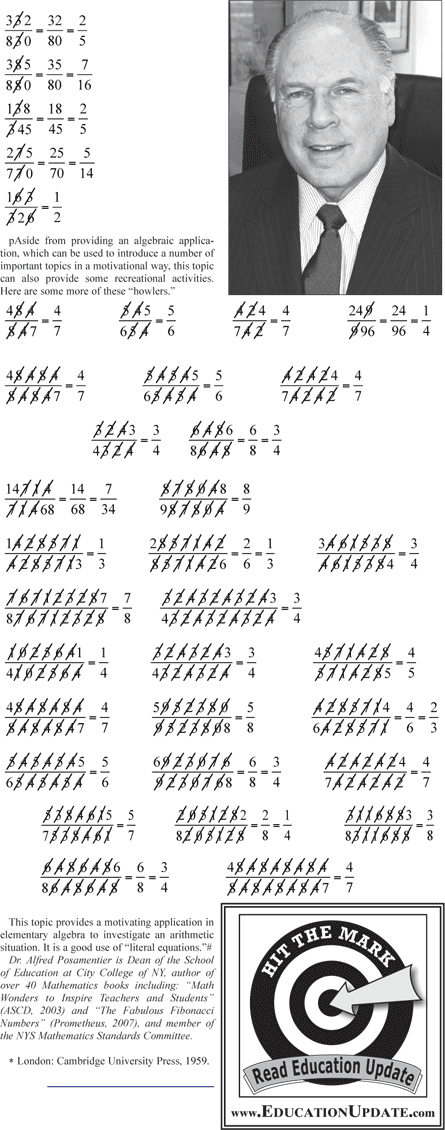
Howlers
by alfred Posamentier, Ph.d.
Now that the summer is upon us, we need to seek some recreation in mathematics. Here is one that will entertain you and will give you some insight into the nature of numbers. So just have fun!
Students sometime provide us with some ideas for exploring mathematical oddities. How often do we see students do something entirely mathematically incorrect and still end up with the correct answer? This could even lead students to justify their wrong work because it produced the right result. Let’s consider the reduction of fractions.
In his book, Fallacies in Mathematics*, E.A. Maxwell refers to the following cancellations as howlers:
Begin your presentation by asking students to reduce to lowest terms the following fractions:
After they have reduced to lowest terms each of the fractions in the usual manner, ask why they didn’t simply do it in the following way:
At this point your students will be somewhat amazed. Their first reaction is probably to ask if this may be done to any fraction composed of two-digit numbers of this sort. Challenge your students to find another fraction (comprised of two-digit numbers) where this type of cancellation will work. Students might cite (55/55) = (5/5) = 1 as an illustration of this type of cancellation. Indicate to them that although this will hold true for all multiples of eleven yielding two-digit results, it is trivial, and our concern will be only with proper fractions (i.e. whose value is less than one).
For a better class, or one that has a good working knowledge of elementary algebra, you may wish to “explain” this situation. That is, why are the four fractions above the only ones (composed of two-digit numbers) where this type of cancellation will hold true?
Have students consider the fraction (10x + a) / (10a + y)
The above four cancellations were such that when canceling the a’s the fraction was equal to x/y.
Therefore, ((10x + a)/(10a + y)) = x/y.
This yields: y(10x + a) = x (10a + y)
10xy + ay = 10 ax + xy
9xy + ay = 10 ax
And so y = (10ax) / (9x + a)
At this point have students inspect this equation. They should realize that it is necessary that x, y and a are integers since they were digits in the numerator and denominator of a fraction. It is now their task to find the values of a and x for which y will also be integral.
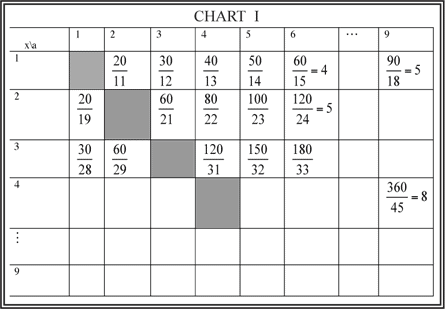
To avoid a lot of algebraic manipulation you might have students set up a chart which will generate values of y from y = (10ax) / (9x + a)
Remind them that x, y and a must be single digit integers. Below is a portion of the table they will construct (SEE CHART I below). Notice that the cases where x = a are excluded since (x/a) = 1.
The portion of Chart I already generated two of the four integral values of y; that is, when x = 1, a = 6, then y = 4, and when x = 2, a = 6, and y = 5. These values yield the fractions 16/64 and 26/65, respectively. The remaining two integral values of y will be obtained when x = 1, and a = 9, yielding y = 5, and when x = 4 and a = 9, yielding y = 8. These yield the fractions 19/95 and 49/98, respectively. This should convince students that there are only four such fractions composed of two-digit numbers.
Students may now wonder if there are fractions composed of numerators and denominators of more than two digits, where this strange type of cancellation holds true. Have students try this type of cancellation with 499/998. They should find that
Soon they will realize that
Enthusiastic students may wish to justify these extensions of the original howlers. Students who at this point have a further desire to seek out additional fractions which permit this strange cancellation should be shown the following fractions. They should verify the legitimacy of this strange cancellation and then set out to discover more such fractions.
pAside from providing an algebraic application, which can be used to introduce a number of important topics in a motivational way, this topic can also provide some recreational activities. Here are some more of these “howlers.”
This topic provides a motivating application in elementary algebra to investigate an arithmetic situation. It is a good use of “literal equations.”#
Dr. Alfred Posamentier is Dean of the School of Education at City College of NY, author of over 40 Mathematics books including: “Math Wonders to Inspire Teachers and Students” (ASCD, 2003) and “The Fabulous Fibonacci Numbers” (Prometheus, 2007), and member of the NYS Mathematics Standards Committee.
* London: Cambridge University Press, 1959.
